B*Tree 인덱스
B*Tree 인덱스 구조 이해
vpn_key 대용량 데이터를 효율적으로 검색, 삽입, 삭제하기 위해 사용하는 자가 균형 이진 탐색 트리
- (중요) 어떤 노드에서든 리프 노드까지의 거리가 항상 일정하게 유지되어 탐색 시간이 일정함.(3D 입체적 탐색)
playlist_add_check오라클 B*tree 인덱스의 특징
- 루트(Root) 노드: 트리의 최상위 노드.
- 브랜치(Branch) 노드: 루트와 리프 노드 사이에 위치하며, 자식 노드를 가리키는 포인터를 포함합니다.
- 리프(Leaf) 노드: 트리의 가장 아래에 위치하며, 인덱스 키와 해당 데이터가 저장된 **ROWID(실제 데이터의 물리적 주소)**를 포함합니다. 리프 노드는 서로 양방향으로 연결되어 있어 인덱스 범위를 순차적으로 스캔하는 데 유리합니다.
- 페이지(Page): B*tree의 각 노드는 물리적으로 페이지 또는 블록이라 불리는 단위에 저장됩니다.
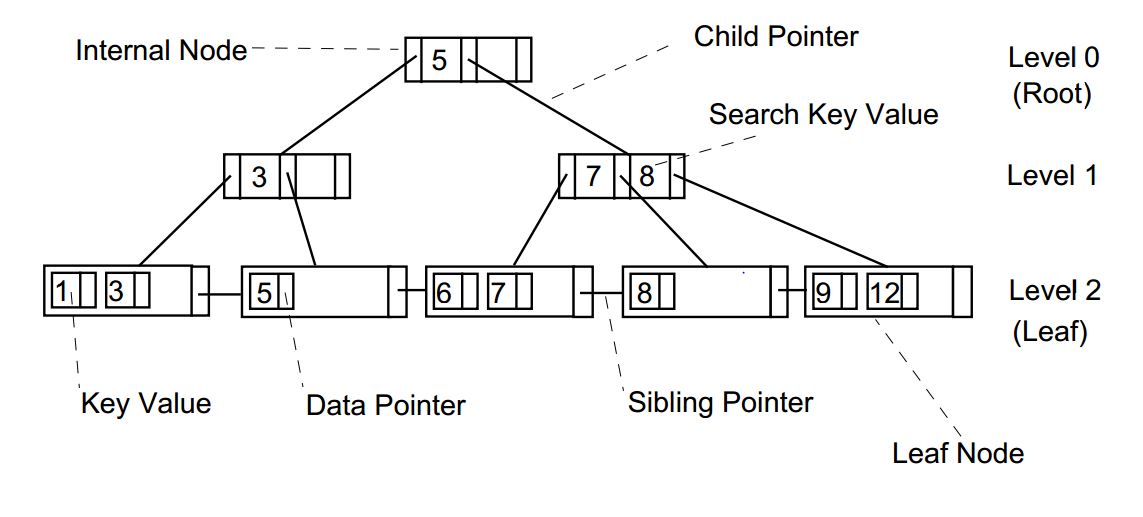
인덱스 작동 방식
데이터 추가시 작동 방식
- 테이블에 데이터가 입력되면 해당 테이블에 존재하는 인덱스에도 추가된 데이터의 인덱스 엔트리가 추가된다.
- 테이블에 추가되는 데이터의 인덱스 키(Key) 값의 저장 위치를 찾기 위해 인덱스 리프 블록을 확인해 찾는다.
- 인덱스 블록의 여유 공간에 해당 인덱스 엔트리를 추가한다.
- 해당 인덱스 블록에 여유 공간이 없을 경우, 해당 블록은 2개의 인덱스 리프 블록으로 분기돼 인덱스 키들은 다시 정렬하고 분기된 2개의 인덱스 리프 블록을 통해 추가된다. 이 때 리프 블록을 연결하고 있는 브랜치 블록과 루트 블록의 정보가 갱신될 수 있다.
데이터 삭제시 작동 방식
- 데이터입력시 발생되는 작동방식과 정반대의 작업을 수행한다.
- 데이터가 삭제되면 해당 인덱스 엔트리의 연결이 끊어진다.그렇게 함으로써 루트 블록으로부터 해당 인덱스 엔트리를 인식하지 못하게 한다.
- 삭제된 인덱스 엔트리의 공간은 추가를 위해 공간 해제를 수행하게 되며, 리프 블록에 하나의 인덱스 엔트리라도 남게 되면 인덱스 리프 블록은 유지되게 된다.
- 많은 인덱스 엔트리가 삭제되면 삭제된 공간은 반납된다.그러나 해당 리프 블록의 전체 데이터가 삭제되지 않는 한 해당 리프 블록은 반납되지 않는다.
- 해당 리프 블록에 새로운 인덱스 엔트리가 추가로 저장되지 않는다면 공간이 낭비되게 된다.
갱신 Update Operation
- 삭제와 추가 작업이 동시에 수행되는 작업이다.
- 테이블에 데이터가 순차적으로 증가해 추가되는 경우 인덱스의 우측으로 인덱스 엔트리가 집중돼 B*TREE의 가장 중요한 특징인 균형(Balance)이 무너지게 된다.
- 또한 죄측 리프 블록으로 인덱스 엔트리가 추가되지 않기 때문에 좌측 리프 블록은 "블록 사용률" 이 낮아지게 된다.
- 삭제가 많거나 또는 인덱스 키가 순차적으로 증가하며 추가되는 테이블은 주기적인 인덱스 재구성(Rebuild)을 통해 인덱스 균형(Balance)을 유지시켜줘야 한다.
B*Tree 인덱스 장점
- 인덱스를 이용해 데이터에 엑세스할 때 모든 인덱스 엔트리에 대해 균형(Balance)을 맞춤
- 인덱스를 이용한 범위(Range) 스캔 시 Double Linked List를 사용하기 때문에 다른 인덱스보다 더 유리하며 ACESENDING과 DESCENDING도 가능함
- OLTP 환경에서 적은 데이터에 엑세스하는 데 유리함
B*Tree 인덱스 단점
- 분포도(Cardinality)가 낮은 컬럼(예 남,여 구분(M,F) 이나 사용여부(Y,N) 같은)의 경우 B*TREE 인덱스가 불리함
- OR 연산자에 대해 테이블 전체를 스캔(Full Scan)하는 것은 위험함
- 인덱스 연산 불가
- 인덱스 확장 시 부하 발생
B*Tree 인덱스 작동 방식을 파이썬으로 구현
- 오라클 B-tree 인덱스의 구조를 핵심적인 개념을 담은 간소화된 예제입니다.
- 아래 코드는 실제 오라클의 복잡한 B-tree를 완벽하게 모방하지는 않지만, 그 작동 원리(노드 분할, 탐색, 삽입)를 이해하는 데 도움이 되는 뼈대를 제공합니다.
💻 파이썬으로 B-Tree 인덱스 구현하기
- 아래 코드는 BTree 클래스를 중심으로 Node 클래스를 사용하여 B-tree의 핵심 기능을 구현합니다.
- 이 예제에서는 노드당 최대 3개의 키를 가질 수 있는 2-3-4 B-tree를 기반으로 합니다.
노드 클래스 (Node)
- 각 노드의 정보를 담는 클래스입니다.
class Node:
def __init__(self, is_leaf=False):
self.keys = [] # 노드에 저장된 키 값 (인덱스 키)
self.children = [] # 자식 노드 (브랜치 노드인 경우)
self.is_leaf = is_leaf # 리프 노드인지 여부
self.rowids = [] # 리프 노드에만 있는 실제 데이터의 주소 (예시)
B-Tree 클래스 (BTree)
- 실제 B-tree의 동작을 담당하는 클래스입니다. 삽입, 탐색, 노드 분할 등의 로직을 포함합니다.
class BTree:
def __init__(self, t):
self.t = t # 최소 차수. 노드당 최소 t-1, 최대 2t-1개의 키를 가짐
self.root = Node(is_leaf=True)
# B-tree에 키와 ROWID를 삽입하는 메서드
def insert(self, key, rowid):
root = self.root
# 루트 노드가 가득 찼을 경우 분할
if len(root.keys) == (2 * self.t) - 1:
temp = Node()
self.root = temp
temp.children.append(root)
self._split_child(temp, 0)
self._insert_non_full(temp, key, rowid)
else:
self._insert_non_full(root, key, rowid)
# 가득 차지 않은 노드에 키 삽입
def _insert_non_full(self, node, key, rowid):
i = len(node.keys) - 1
if node.is_leaf:
# 리프 노드에 키와 rowid 삽입
while i >= 0 and key < node.keys[i]:
i -= 1
node.keys.insert(i + 1, key)
node.rowids.insert(i + 1, rowid)
else:
# 브랜치 노드에 키 삽입
while i >= 0 and key < node.keys[i]:
i -= 1
i += 1
# 자식 노드가 가득 찼으면 분할
if len(node.children[i].keys) == (2 * self.t) - 1:
self._split_child(node, i)
if key > node.keys[i]:
i += 1
self._insert_non_full(node.children[i], key, rowid)
# 자식 노드 분할
def _split_child(self, parent_node, i):
t = self.t
child_node = parent_node.children[i]
# 새로운 노드 생성
new_node = Node(is_leaf=child_node.is_leaf)
# 부모 노드로 중간 키 이동
parent_node.keys.insert(i, child_node.keys[t - 1])
parent_node.children.insert(i + 1, new_node)
# 새 노드로 키와 rowid 이동
new_node.keys = child_node.keys[t:]
child_node.keys = child_node.keys[:t - 1]
if child_node.is_leaf:
new_node.rowids = child_node.rowids[t:]
child_node.rowids = child_node.rowids[:t - 1]
else:
new_node.children = child_node.children[t:]
child_node.children = child_node.children[:t]
# B-tree에서 키를 탐색하는 메서드
def search(self, key):
return self._search_node(self.root, key)
# 재귀적으로 노드를 탐색
def _search_node(self, node, key):
i = 0
while i < len(node.keys) and key > node.keys[i]:
i += 1
if i < len(node.keys) and key == node.keys[i]:
# 키를 찾았을 경우 해당 ROWID 반환 (리프 노드인 경우)
if node.is_leaf:
return node.rowids[i]
# 브랜치 노드인 경우, 키를 찾았더라도 자식 노드로 이동 (중복 키 처리)
else:
return self._search_node(node.children[i], key)
if node.is_leaf:
return None # 키가 존재하지 않음
else:
return self._search_node(node.children[i], key)
# B-tree 구조를 출력하는 메서드 (디버깅용)
def print_tree(self, node=None, level=0):
if node is None:
node = self.root
print(" " * level + "Level {}: Keys {}".format(level, node.keys))
if not node.is_leaf:
for child in node.children:
self.print_tree(child, level + 1)
사용 예제
- 위에서 만든 B-tree 클래스를 사용하여 인덱스를 구축하고 탐색하는 과정을 시뮬레이션해봅니다.
if __name__ == "__main__":
b_tree = BTree(t=2) # 2-3 B-tree (노드당 최대 3개 키)
# 인덱스에 키와 가상의 ROWID 삽입
keys = [10, 20, 5, 6, 12, 30, 7, 17]
for i, key in enumerate(keys):
b_tree.insert(key, f"rowid_{i}")
print("=== B-tree 인덱스 구조 ===")
b_tree.print_tree()
print("\n" + "="*30)
print("=== 키 탐색 ===")
search_key = 6
result_rowid = b_tree.search(search_key)
print(f"키 {search_key}에 대한 ROWID: {result_rowid}")
search_key = 25
result_rowid = b_tree.search(search_key)
print(f"키 {search_key}에 대한 ROWID: {result_rowid}")
# 출력 결과 예시:
# === B-tree 인덱스 구조 ===
# Level 0: Keys [10, 20]
# Level 1: Keys [5, 6, 7]
# Level 1: Keys [12, 17]
# Level 1: Keys [30]
#
# ==============================
# === 키 탐색 ===
# 키 6에 대한 ROWID: rowid_3
# 키 25에 대한 ROWID: None
📝 코드 해설
- BTree(t=2): t는 B-tree의 **최소 차수(minimum degree)**를 의미합니다.
- t=2는 노드당 최소 1개, 최대 3개의 키를 가질 수 있음을 뜻합니다.
- 오라클의 실제 B-tree는 훨씬 높은 차수를 사용해 노드당 더 많은 키를 저장합니다.
- insert(key, rowid): 새로운 키를 트리에 삽입하는 메서드입니다.
- 루트 노드가 가득 찼을 때 트리의 높이를 증가시키기 위해 루트 노드를 분할하는 로직이 포함되어 있습니다.
- _insert_non_full(node, key, rowid): 재귀적으로 적절한 위치를 찾아 키를 삽입하는 내부 메서드입니다.
- 삽입하려는 노드가 리프 노드인지, 아니면 브랜치 노드인지에 따라 다른 로직을 수행합니다.
- _split_child(parent_node, i): B-tree의 핵심적인 동작 중 하나로, 노드가 가득 찼을 때 중간 키를 부모 노드로 올리고 두 개의 자식 노드로 분할하는 로직을 구현합니다. 이 과정을 통해 트리의 균형이 유지됩니다.
- search(key): 주어진 키를 트리를 따라 내려가며 찾는 메서드입니다. 키를 찾으면 해당 ROWID를 반환하고, 찾지 못하면 None을 반환합니다.
이 코드는 오라클 B-tree의 기본 원리를 설명하기 위한 예제이며, 실제 오라클 데이터베이스의 복잡한 인덱스 관리, 동시성 제어, 트랜잭션 처리와 같은 기능은 포함하고 있지 않습니다.